El número áureo
Nuestra sociedad no puede existir sin los números. Ahora más que nunca ,vivimos en un mundo que se levanta sobre los números:π,е,…
Uno de los más interesantes es el número 1’6180339887…. Este número es llamado de muchas maneras: número de oro, proporción trascendental, número divino, divina proporción,… Y se representa con la letra griega Φ (phi)
Reproducir sus cifras en letra impresa resultaría literalmente imposible, y no porque sea excesivamente grande (ya que apenas es mayor que 1),sino porque está compuesto por infinitos dígitos que no siguen pauta alguna.
Dato interesante: Si cogemos por ejemplo 10.000 de sus decimales y buscamos en ello, tropezaremos con toda seguridad con nuestra fecha de nacimiento, pero también con la matricula de nuestro coche. En realidad, podemos encontrar cualquier tipo de secuencia numérica que podamos imaginar
Su anotación aritmética es:
Es un número irracional, lo que quiere decir que nunca podremos tener una expresión decimal exacta y que no habrá ningún grupo de sus decimales que se repita periódicamente
Aproximación geométrica
Sucesión de Fibonacci
1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,…
Cada número se genera con la suma de los anteriores. El cociente entre un término cualquiera de la sucesión y su antecedente se aproxima a Φ
El número de oro aparece en un libro llamado “Elementos de la Geometría” de un matemático llamado Euclides de a.C. En ese libro se dice que una recta está dividida en media y extrema razón, cuando la longitud de la línea total es a la de la parte mayor, como la de esta parte mayor es a la de la menor, es decir, el todo es a la parte como la parte al resto.
x=1’618
Puesto que la solución de la ecuación es la relación entre las longitudes de los segmentos, esa será la misma, cualquiera que sea el segmento del que partamos, es decir, la proporción áurea tendrá el mismo valor con independencia de la longitud del segmento inicial.
Propiedades elementales de Φ
#1/Φ=Φ-1Ahora multipliquemos en la segunda propiedad varias veces por Φ en los dos miembros
“Cualquier potencia de Φ es igual a la suma de las dos potencias anteriores”
#Luego , una vez que tengamos los valores de Φ y su cuadrado, si queremos obtener el resto de potencias, basta con ir sumando dos consecutivas para obtener la siguiente.
#Del mismo modo, utilizando las 3 propiedades podemos encontrar otras equivalencias para las potencias en las que sólo interviene Φ y números naturales.#Volviendo a Fibonacci, este escribió otro libro titulado “Libro del Ábaco” donde se encuentra el problema de los conejos cuyo enunciado es: ¿Cuántas parejas de conejos tendremos a fin de año si comenzamos con una pareja que produce cada mes otra pareja que procrea a su vez a los dos meses de vida?
#En su resolución se encuentra la sucesión de Fibonacci ya expuesta con anterioridad.
#Así que la respuesta al ejercicio, acerca de cuántas parejas de conejos habrá luego de un año, resulta ser el doceavo término de la sucesión: 144.
#Del mismo modo, utilizando las 3 propiedades podemos encontrar otras equivalencias para las potencias en las que sólo interviene Φ y números naturales.#Volviendo a Fibonacci, este escribió otro libro titulado “Libro del Ábaco” donde se encuentra el problema de los conejos cuyo enunciado es: ¿Cuántas parejas de conejos tendremos a fin de año si comenzamos con una pareja que produce cada mes otra pareja que procrea a su vez a los dos meses de vida?
#En su resolución se encuentra la sucesión de Fibonacci ya expuesta con anterioridad.
#Así que la respuesta al ejercicio, acerca de cuántas parejas de conejos habrá luego de un año, resulta ser el doceavo término de la sucesión: 144.
Relación entre el numero áureo y Fibonacci
Relaciones numéricas sorprendentes
#Suma de los términos de la sucesión de Fibonacci: Si elegimos diez términos consecutivos cualquiera de la sucesión y los sumamos, veremos que siempre obtenemos un múltiplo de 11( si esto lo estudiamos a fondo nos podemos llevar grandes sorpresas) #Las ternas pitagóricas: si cogemos tres números de la sucesión de Fibonacci podremos comprobar fácilmente que forman una terna pitagórica:
Marta Garduño García






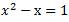







No hay comentarios:
Publicar un comentario